To go along with how I’m understanding your “trick” coin analogy: 2 consecutive coin flips. One with a heads/tails coin. The second flip is with either another heads/tails coin or with a tails/tails coin. If the first flip is heads, we get the fair coin, if the first flip is tails we get the “trick” coin. Some honest referee is flipping the coins as prescribed, but we can’t see the results of the flips.
The first flip is our 100% het bred to a normal. The second is the 50% pos het to another normal.
At the end of the second flip in the game above, what is the probability that the result of that flip is heads? Is that impossible to quantify?
For that second flip the conditional probability of Heads given the second coin is the “trick” coin is 0%
Also, for the second flip the conditional probability of Heads given the fair coin is 50%
But we are interested simply in “what is the probability the second flip is heads.”
We don’t know the exact condition we are in after the first flip though, so we can’t rely completely on the conditional probabilities. But we do know the probability for being in each of the conditions for those conditional probabilities: in this game it’s 50/50.
The way the math works out for this:
probability of H2 = (probability of H2 given H1) * (probability of H1) + (probability of H2 given T1) * (probability of T1) = 0.5*0.5 + 0*0.5 = 0.25
So yes, breeding a 50% het to a normal means that every hatchling in that clutch has a 25% chance of having inherited the het gene. Further observations of genetic interactions can update this belief for all the animals involved. But as it stands after that pairing: it is certainly honest, theoretically, and mathematically correct to state that there is a 25% probability, chance, odds, that those snakes have the gene. *assuming we can ignore the probabilities for other genetic mechanisms; which I am certainly no expert on

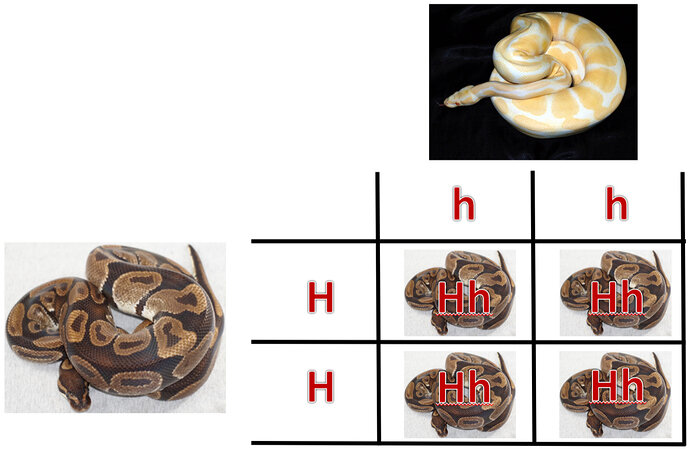
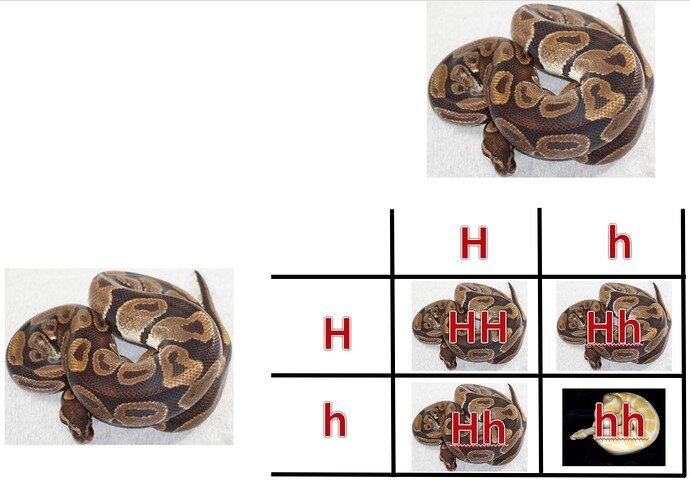
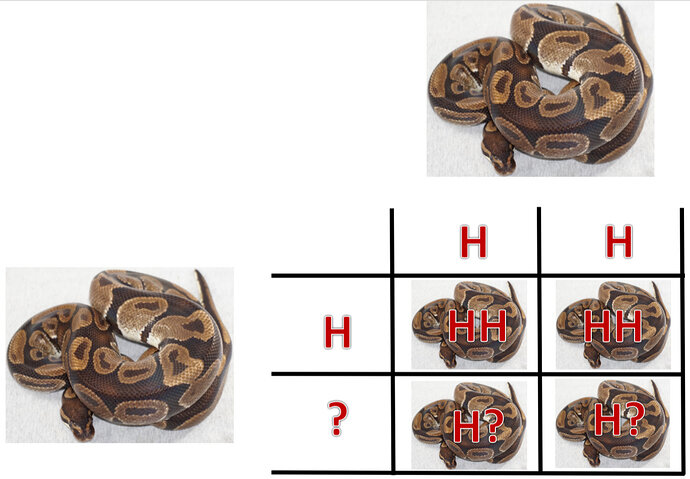

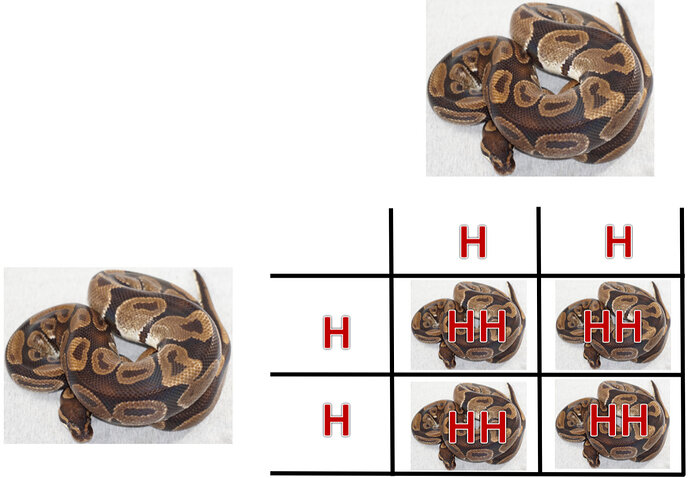
 i have never had a problem with understanding how genes work when it comes to basics like het to het, visual to het and visual to visual. That’s all fairly simple.
i have never had a problem with understanding how genes work when it comes to basics like het to het, visual to het and visual to visual. That’s all fairly simple.